Пребарување се нарекува процесот на барање на даден елемент од дадена структура на податоци. До
бараниот елемент може да се пристапи на различни начини, кои се помалку или повеќе ефикасни.
Ќе разгледаме пребарување во несортирани и сортирани низи.
Линеарно пребарување
Несортирани низи
Со линеарното пребарување бараниот елемент се споредува со секој елемент на низата. Кога ќе се
пронајде бараниот елемент, алгоритмот завршува и го враќа индексот на тој елемент, а доколку нема
таков елемент, алгоритмот враќа соодветна порака. Карактеристична операција на овој начин на
пебарување е споредувањето. Овој алгоритам има линеарна временска сложеност, O(n). Просечниот
број на споредби е (n+1)/2 а најлошиот случај е n споредби.
Линеарното пребарување може да се примени и на сортирана низа. Придобивка овде е тоа што
доколку бараниот елемент го нема во низата, не мора да бараме до крај на низата, туку до првиот
елемент поголем од бараниот (освен ако бараниот елемент не е поголем од сите елементи од низта ).
Истотака ако бараниот елемент е помал од првиот тогаш него го нема во низата.
#include<iostream>
using namespace std;
int search(int arr[], int n, int x)
{
int i;
for (i = 0; i < n; i++)
if (arr[i] == x)
return i;
return -1;
}
// Driver code
int main()
{
int arr[] = { 2, 3, 4, 10, 40 };
int x = 10;
int n = sizeof(arr) / sizeof(arr[0]);
// Function call
int result = search(arr, n, x);
if (result == -1)
cout << "Element is not present in array";
else cout << "Element is present at index " << result;
return 0;
}
Примери
Linear Search in C++
#include <iostream>
using namespace std;
void linearno(int a[], int m, int i, int n)
{ int t = 0;
for (i = 0; i < n ; i++)
if (m == a[i] )
{ t= 1; break; }
if (t == 1)
cout<<"Elementot e na pozicija "<<i;
else
cout<<"Elementot ne e prisuten vo nizata.";
}
int main()
{ int n, a[100];
int i, m, t = 0;
cout<<"Vnesi go n ";
cin>>n;
cout<<"Vnesi gi elementite"<<endl;
for (i = 0; i < n; i++)
cin>> a[i];
cout<<"Vnesi go elementot sto go baras ";
cin>>m;
linearno(a, m,i,n);
return 0;
}Output:Vnesi go n 5 Vnesi gi elementite 1 3 -2 45 7 Vnesi go elementot sto go baras 2 Elementot ne e prisuten vo nizata.
Vnesi go n 4 Vnesi gi elementite 9 0 -2 1 Vnesi go elementot sto go baras 0 Elementot e na pozicija 1
Linear Search with Duplicate Element
#include<iostream> using namespace std; int main() { int arr[100], tot, i, num, arrTemp[50], j=0, chk=0; cout<<"Enter the Size for Array Size: "; cin>>tot; cout<<"Enter "<<tot<<" Array Elements: "; for(i=0; i<tot; i++) cin>>arr[i]; cout<<"\nEnter the Number to Search: "; cin>>num; for(i=0; i<tot; i++) { if(arr[i]==num) { arrTemp[j] = i; j++; chk++; } } if(chk>0) { cout<<"\nNumber Found at Index No. "; tot = chk; for(i=0; i<tot; i++) cout<<arrTemp[i]<<" "; } else cout<<"\nNumber doesn't Found!"; cout<<endl; return 0; }Enter the Size for Array Size: 5 Enter 5 Array Elements: 1 3 45 1 1 Enter the Number to Search: 1 Number Found at Index No. 0 3 4We have implemented a linear search using C++
#include <iostream>#include <string>usingnamespacestd;intmain(){intmyarray[10] = {21,43,23,54,75,13,5,8,25,10};intkey,loc;cout<<"The input array is"<<endl;for(inti=0;i<10;i++){cout<<myarray[i]<<" ";}cout<<endl;cout<<"Enter the key to be searched : "; cin>>key;for(inti = 0; i< 10; i++){if(myarray[i] == key){loc = i+1;break;}elseloc = 0;}if(loc != 0){cout<<"Key found at position "<<loc<<" in the array";}else{cout<<"Could not find given key in the array";}}Output:
The input array is
21 43 23 54 75 13 5 8 25 10
Enter the key to be searched : 3
Could not find given key in the arrayThe input array is
21 43 23 54 75 13 5 8 25 10
Enter the key to be searched: 75
Key found at position 5 in the array
Бинарно пребарување
Поефикасно пребарување на сортираните низи е бинарното пребарување.
Бинарно пребаруваме имаме кога бараме збор во речник. На почеток го отвораме речникот на средина и ако ја
погодиме страната застануваме. Но ако не ја погодиме страната, во зависност од тоа дали почетната
буква на бараниот збор е пред или по буквата на која сме наиделе, повторно отвораме во првата или
втората половина на речникот итн. се до наоѓањето на зборот.
Поточно постапката се одвива на следниот начин:
1. Постави dolna=1( или 0) и gorna=n ( или n-1) ( каде n е бројот на елементи на низата)
2. Додека dolna<=gornа повторувај
2.1 Постави sredina=(dolna + gorna) /2
2
2 Ако бараниот елемент е a[sredina] заврши со излез sredina
2.3 Ако бараниот елемент е помал од a[sredina] тогаш gorna=sredina-1
2.4 Ако бараниот елемент е поголем од a[sredina] тогаш dolna=sredina-1
3. Заврши со излез 0
Бројот на итерации на овој алгоритам во најлош случај е еднаков на бројот на делење на должината
на низата со два се додека должината не стане нула т.е Log2n па и временската сложеност е O(Log2n).
Програма која печати на која позиција е првото појавување на даден број во еднодимензионална низа а со н елементи. Ако елементот не е во низата, да се даде соодветна порака
#include <iostream>
#include <conio.h>
using namespace std;
int main()
{
int n, l, mid, h, key;
cout << "Enter size of the array: ";
cin >> n;
cout << endl;
int A[n];
cout <<"Enter elements of the array:\n";
for (int i = 0; i < n; i++)
{
cin >> A[i];
}
cout <<"\nEnter the key Element: ";
cin >> key;
cout << endl;
l = 0;
h = n - 1;
while(l <= h)
{
mid = (l + h) / 2;
if(key == A[mid])
{
cout << "Key: " << key << " found at " << mid << endl;
return 0;
}
else if (key < A[mid])
h = mid - 1;
else
l = mid + 1;
}
cout << key << " not Found";
getch ();
}
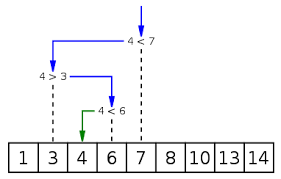
#include using namespace std; int binarySearch(int arr[], int p, int r, int num) { if (p <= r) { int mid = (p + r)/2; if (arr[mid] == num) return mid ; if (arr[mid] > num) return binarySearch(arr, p, mid-1, num); if (arr[mid] < num) return binarySearch(arr, mid+1, r, num); } return -1; } int main(void) { int arr[] = {1, 3, 7, 15, 18, 20, 25, 33, 36, 40}; int n = sizeof(arr)/ sizeof(arr[0]); int num; cout << "Enter the number to search: \n"; cin >> num; int index = binarySearch (arr, 0, n-1, num); if(index == -1){ cout<< num <<" is not present in the array"; }else{ cout<< num <<" is present at index "<< index <<" in the array"; } return 0; }
Output
Enter the numberto search
20
20 is present at index 5 in the array#include <iostream>#include <string>using namespace std;int binarySearch(int myarray[], int beg, int end, int key) { int mid; if(end >= beg) { mid = (beg + end)/2; if(myarray[mid] == key) { return mid+1; } else if(myarray[mid] < key) { return binarySearch(myarray,mid+1,end,key); } else { return binarySearch(myarray,beg,mid-1,key); } } return -1; } int main () { int myarray[10] = {5,8,10,13,21,23,25,43,54,75}; int key, location=-1; cout<<"The input array is"<<endl; for(int i=0;i<10;i++){ cout<<myarray[i]<<" "; } cout<<endl; cout<<"Enter the key that is to be searched:"; cin>>key; location = binarySearch(myarray, 0, 9, key); if(location != -1) { cout<<"Key found at location "<<location; } else { cout<<"Requested key not found"; } } |
Output:
The input array is
5 8 10 13 21 23 25 43 54 75
Enter the key that is to be searched:21
Key found at location 5
Задачи
1. Програма што ќе пресмета и печати колку од броевите во еднодимензионална низа со n
елементи, се едноцифрени, колку се двоцифрени, а колку се трицифрени.
2. Програма со која од дадена еднодимензионална низа со н елементи креира други две низи,
едната составена од парните, а другата од непарните елементи на низата а
3. Состави програма со која од дадена еднодимензионална низа со n елементи се креираат други две низи, едната составена од елементите од првата десетка, а другата од останатите елементи на низата а.
No comments:
Post a Comment